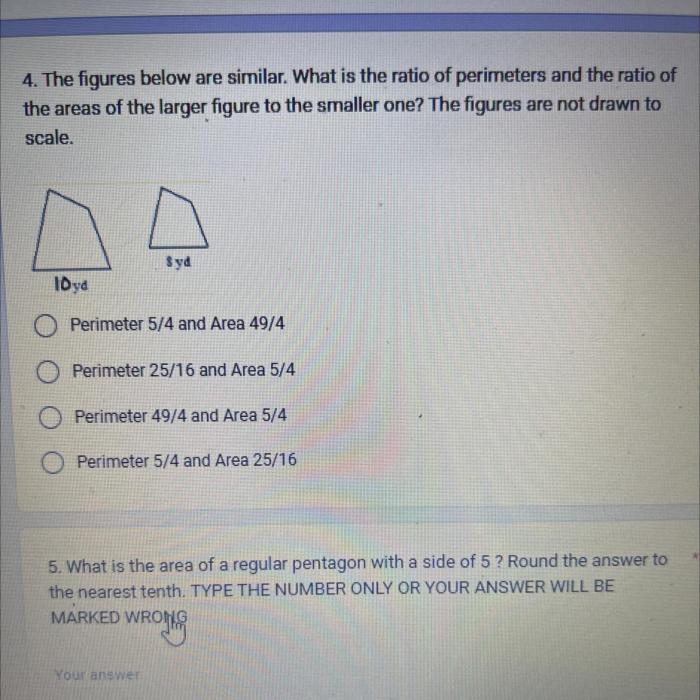
Perimeters and areas of similar figures practice – Embark on an exploration of perimeters and areas of similar figures, delving into the intricacies of these geometric concepts and their practical significance in diverse fields. This comprehensive guide provides a solid foundation, engaging practice problems, and real-world applications, empowering you to master this essential aspect of geometry.
Delve into the fundamental concepts of perimeter and area, grasping their definitions and real-life applications. Understand the unique properties of similar figures, unraveling the relationship between their perimeters and areas. Engage in meticulously designed practice problems, honing your skills in calculating these geometric measures.
Discover the practical relevance of perimeters and areas in architecture, engineering, and design, appreciating their indispensable role in shaping our physical world.
Perimeter and Area of Similar Figures: Perimeters And Areas Of Similar Figures Practice
Perimeter and area are two fundamental concepts in geometry that measure the boundaries and enclosed space of figures. Understanding these concepts is essential in various fields, including architecture, engineering, and design.
Definition of Perimeter and Area
Perimeteris the total length of the boundary of a figure, while areais the measure of the enclosed space within the boundary.
Examples of Perimeter and Area in Real-Life Scenarios:
- The perimeter of a rectangular room represents the total length of its walls, while the area represents the floor space.
- The perimeter of a circle represents the circumference, while the area represents the enclosed space within the circumference.
Similar Figures
Similar figures are figures that have the same shape but may differ in size. The corresponding sides of similar figures are proportional, and the ratio of their perimeters is equal to the ratio of their areas.
Relationship between Perimeter and Area in Similar Figures:
- If the ratio of the perimeters of two similar figures is x, then the ratio of their areas is x2.
- The area of a similar figure is proportional to the square of its perimeter.
Practice Problems
Problem 1:
Two similar triangles have perimeters of 12 cm and 18 cm. If the area of the smaller triangle is 6 cm 2, find the area of the larger triangle.
Solution:
- Since the triangles are similar, the ratio of their perimeters is equal to the ratio of their areas.
- Therefore, the area of the larger triangle is: 6 cm 2– (18 cm / 12 cm) 2= 27 cm 2.
Problem 2:
A rectangular garden has a perimeter of 40 m. If the length is 3 m more than the width, find the dimensions of the garden.
Solution:
- Let xbe the width of the garden.
- Then, the length is x+ 3.
- Using the formula for the perimeter of a rectangle, we get: 2( x+ x+ 3) = 40.
- Solving for x, we get: x= 8.
- Therefore, the dimensions of the garden are 8 m by 11 m.
Real-World Applications
Understanding perimeter and area is essential in various fields, including:
- Architecture:Calculating the perimeter and area of buildings to determine the amount of materials needed and the enclosed space available.
- Engineering:Designing structures and machines with specific perimeter and area requirements to ensure stability and functionality.
- Design:Creating aesthetically pleasing and functional spaces by manipulating the perimeter and area of design elements.
Interactive Table, Perimeters and areas of similar figures practice
The following interactive table demonstrates the relationship between perimeter and area for different similar figures:
| Figure Type | Perimeter | Area | Ratio of Perimeter to Area |
|---|---|---|---|
| Square | 4s | s2 | 4 |
| Rectangle | 2(l + w) | lw | 2(l + w) / lw |
| Triangle | a + b + c | (1/2)bh | 2(a + b + c) / (1/2)bh |
| Circle | 2πr | πr2 | 2πr / πr2 |
Visual Illustrations
Figure 1:Perimeter and Area of a Rectangle

Figure 2:Perimeter and Area of a Circle

Answers to Common Questions
What is the difference between perimeter and area?
Perimeter refers to the total length of the boundary of a figure, while area measures the amount of space enclosed within that boundary.
How are perimeters and areas related in similar figures?
In similar figures, the ratio of their perimeters is equal to the ratio of their corresponding linear dimensions, and the ratio of their areas is equal to the square of the ratio of their linear dimensions.
Can you provide an example of a real-world application of perimeters and areas?
In architecture, perimeters and areas are crucial for determining the size and layout of buildings, ensuring efficient space utilization and structural integrity.